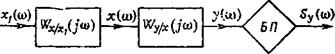МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ САМОЛЕТА. В ТУРБУЛЕНТНОЙ АТМОСФЕРЕ

Линейная	Sy{jUi)
система

ной специфической задачи — дина — Рис. 2.7. Линейная система при мики движения самолета в турбу — стационарном случайном воз — лентной атмосфере. При этом счи — мущении

тается, что турбулентность является

стационарным случайным процессом, который описывается ана­литическими выражениями, проведенными в гл. 1.

Движение любой системы, описываемой линейным дифферен­циальным уравнением вида (2.31), под действием стационарного случайного возмущения может быть исследовано хорошо извест­ными методами с использованием аппарата корреляционных функций или спектральных плотностей. В данной книге исполь­зуется аппарат спектральных плотностей. Спектральная плот­ность Sу (со) выходной величины какой-либо системы, имеющей частотную характеристику Wylx(j<a) (рис. 2.7), определяется вы­ражением

5у («) = | Wy/x (/*) |2 Sx (о)) = W2ylx (о>) Sx (Ч (2.46)

где S*((o) —спектральная плотность возмущения.

Спектральная плотность весьма полно характеризует измене­ние выходной величины под действием случайного стационарного воздействия, так как показывает, как распределена по частотам дисперсия выходной величины. Однако на практике чаще огра­ничиваются оценкой изменения выходной величины по ее средне­
квадратичному значению ау, которое связано со спектральной плотностью формулой[15]

При исследовании динамики самолета аналитическое опреде­ление как спектральной плотности, так и среднеквадратичного значения (или дисперсии о„2) является весьма трудоемким про­цессом. Это объясняется сложностью передаточных функций и. следовательно, частотных характеристик самолета.

Для вычисления спектральной плотности и дисперсии пара­метров движения самолета можно использовать аналоговые ма­шины [30]. Определение спектральной плотности выходной вели­чины на аналоговых машинах основано на моделировании соотношения (2.46). Спектральная плотность ветра является дробно-рациональной функцией частоты <о, в которую со входит только в четных степенях. Поэтому спектральную плотность вход­ной величины можно представить в виде квадрата модуля ча­стотной характеристики некоторой линейной системы, обычно называемой формирующим фильтром:

$»= | WxlXl{j*) |2=^к(Ч (2-48)

где х — входная величина исследуемой системы;

Х — синусоидальный сигнал частоты со, подаваемый на вход формирующего фильтра с частотной характеристикой WJxl (/со).

Учитывая (2.48), из (2.46) получаем

Sy (0>)=I Wx, Xx (/CD) Wy, x (/CD) Iа. (2.49)

Из (2.49) следует, что если последовательно соединить модели формирующего фильтра и исследуемой системы и подать на вход фильтра синусоидальный сигнал частоты о>, то квадрат ампли-

Рис. 2.8. Блок-схема моделирования спектральной плотно­сти выходной величины

туды выходного сигнала будет равен спектральной плотности выходной величины исследуемой системы при этой частоте. Блок — схема моделирования спектральной плотности выходной вели­чины приведена на рис. 2.8. Буквами БП на этом рисунке обо-

значен блок перемножения, возводящий в квадрат величи­ну #(<<>)•

Рассмотрим методику определения параметров формирую­щего фильтра для моделирования спектральной плотности воз­мущающего воздействия.

1 + Зд2а>2 (1 + <*2(02)2 ’

В качестве примера возьмем выражение (1.33) для спектраль­ной плотности поперечной составляющей случайного ветра и представим его в более удобной форме:

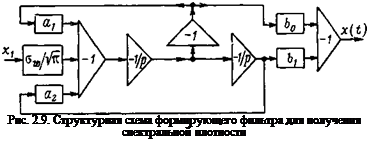Приравняем (2.50) квадрату искомой частотной характерис­тики UP*/*, (/<■>) (2.48):

Нетрудно заметить, что соотношению (2.51) будет удовлетво­рять следующее выражение:

Js—Va 1 ~Ь Z1 ■ 73ам

У~У (1 + /а<о)2

Из (2.52) следует, что передаточная функция формирующего фильтра для поперечной составляющей ветра должна иметь вид

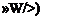
•" <Чр Ya 1 + 1 >73ар __ Vw ЬьР + Ь у2 53)

VI <1 + а/>)2 уп Р^ + йіР+аг

al = 2ja, а2=1/а2, 60=1,73/V«. &i=l/a3’2. (2.54)

Структурная схема моделирования передаточной функции вида (2.53) на аналоговой машине приведена на рис. 2.9.

Необходимо обратить внимание на то, что при использовании фильтра, собранного по схеме рис. 2.9, среднеквадратичному

значению ветра приводится в соответствие амплитуда синусом дального напряжения, подаваемого от инфранизкочастотного ге­нератора. На выходе схемы 2.9 должна измеряться амплитуде напряжения, получающегося после блока перемножения. Ампли­туда синусоидального напряжения на входе должна быть умень­шена в /я раз [формула (2.53)], чтобы формирующий фильтр соответствовал исходному выражению для спектральной плот­ности.

Формирующий фильтр несколько другой схемы может быть использован для получения дисперсии выходных параметров си­стемы, находящейся под воздействием стационарного возму щения.

Определение дисперсии параметров исследуемой системы на аналоговой машине обосновывается соотношением

оо эо

4 = 1 Sy(*)dm = f I WxlXl{j<»Wylx{jm)>d<». (2.55)

о 6

С другой стороны, известно, что частотная характеристика и импульсная переходная функция линейной системы связаны между собой теоремой Релея:

оо оо

5 Ky(t)dt= ±.J I WXIXl(j’4iWyiAn Р<Ь — (2.56) о о

В интеграле левой части теоремы Релея нижний предел —ос заменен на 0, так как импульсная переходная функция Kv(t) при «О тождественно равна нулю.

Правые части (2.55) и (2.56) различаются только коэффици ентом 1/я. Поэтому

оо оо

а2у=5 K2(t)dt=± | V* №Х/Хг (уш) Wy! x (/ш) р dm. (2.57,

о о

Выражение (2.57) показывает, что для получения дисперсии в форме интеграла от квадрата импульсной функции некоторой системы при принятом соотношении (2.47) между дисперсией и спектральной плотностью частотная характеристика этой системы

должна быть умножена на V я.

Формула (2.57) неудобна для моделирования, так как требу ет воздействия на систему импульсной функцией. В обычных интеграторах внешние воздействия задаются в форме единичной функции. Из (2.32) следует, что если Ky(t) есть импульсная пере­ходная функция системы с частотной характеристикой W(j<a), то она же есть переходная функция системы с частотой характе­ристики j<aW(/’©). По этой причине на блок-схеме для модели-

рования дисперсии (рис. 2.10) передаточная функция формирую­щего фильтра имеет дополнительный множитель р, а на вход подается единичная функция. Передаточная функция формирую-

щего фильтра, соответствующего спектральной плотности (2.50), с учетом дополнительных множителей Yк И Р будет иметь вид

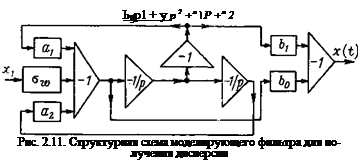(2.58)

Коэффициенты щ и определяются формулами (2.54). Струк­турная схема моделирования этого фильтра приведена на рис. 2.11.

Из выражения (2.57) • следует, что квадрату дисперсии иссле­дуемой величины соответствует напряжение на выходе схемы (рис. 2.10) после окончания пере­ходного процесса, вызванного подачей на вход ступенчатой функции. Теоретически это время равно бесконечности. Практически при исследова­нии динамики самолета оно колеблется в преде­лах единиц или десятков секунд. На рис. 2.12 по­казана типичная осциллограмма выходного на­пряжения схемы (рис. 2.10) при исследовании пе­регрузки, вызываемой случайным вертикальным, J 1

ветром. ^

Приведенная методика моделирования дина­мики системы, на которую действует возмущение, Рис. 2.12. Ос — имеющее характер стационарной случайной функ — циллограмма Ции, дает возможность достаточно быстро иссле — выходе^""^"3 довать движения самолета в турбулентной атмос — схемы на фере. рис. 2.10